Una sorprenent llei matemàtica en els textos del Projecte Gutenberg
19/02/2016
La llei de Zipf en la seva versió més senzilla, formulada als anys 30 pel lingüista estadounidenc George Kingsley Zipf, determina que, de manera sorprenent, la paraula més freqüent d’un text apareix el doble de vegades que la següent més freqüent, tres cops més que la tercera més freqüent, quatre vegades més que la quarta més freqüent, i així successivament.
La llei es pot aplicar en molts altres camps, no només en la literatura, i s’ha comprovat amb més o menys rigor en grans quantitats de dades, però fins ara ha mancat d’una comprovació amb tot el rigor matemàtic i en una base de dades prou gran com per donar validesa estadística.
Investigadors del Centre de Recerca Matemàtica (CRM) –centre de la xarxa CERCA de la Generalitat de Catalunya– adscrits al Departament de Matemàtiques de la UAB, han analitzat per primer cop, amb tot el rigor matemàtic i estadístic necessari, la validesa de la llei de Zipf. Aquest estudi s’emmarca dins el projecte “Recerca en Matemàtica Col·laborativa”, impulsat per l’Obra Social “la Caixa”. Per aconseguir-ho, han analitzat tota la col·lecció de textos en llengua anglesa del projecte Gutenberg, una base de dades pública i gratuita amb més de 30.000 obres en aquesta llengua. Es tracta d’una tasca sense precedents: en l’àmbit de la lingüística la llei mai havia estat comprovada en conjunts de més d’una dotzena de textos.
Segons l’anàlisi, si s’ignoren les paraules més rares, aquelles que només surten un o dos cops en tot un llibre, el 55% dels textos s’ajusten perfectament a la llei de Zipf (en la seva formulació més general). Si es tenen en compte totes les paraules, també les més rares, aquest percentatge és del 40%.
“És molt sorprenent que la freqüència d’aparició de les paraules estigui determinada per una fórmula amb un sol paràmetre lliure. La famosa campana de Gauss, per exemple, ja en necessita dos, posició i amplada, per ajustar-se a les dades reals” explica Álvaro Corral, investigador del CRM adscrit al Departament de Matemàtiques de la UAB i coordinador de la recerca. “Si descartéssim paraules que apareixen 3, 4 o 5 vegades en tota una obra, la proporció de llibres que segueixen la llei de Zipf podria arribar a percentatges encara més alts”.
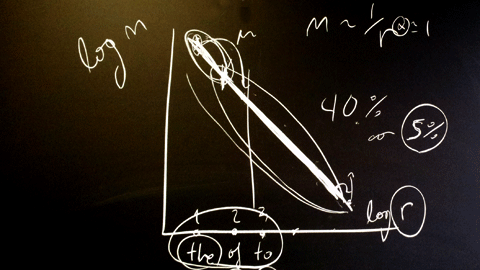
En termes matemàtics, la llei afirma que si s’ordenen totes les paraules per freqüència d’ús, la segona més freqüent apareix ½ vegades el nombre de cops que apareix la més freqüent; la tercera, 1/3 vegades i, en general, la que ocupa la posició n apareix 1/n vegades la més freqüent.
En realitat, la formulació més general de la llei inclou un exponent a, de manera que la relació és 1/na. Tot i complicar una mica la fórmula, la freqüència s’ajusta moltíssim per a valors de “a” molt propers a 1 (és a dir, com si no s’hagués afegit cap exponent). I encara hi ha altres formulacions matemàticament més complexes de la llei, però totes amb un sol paràmetre lliure.
Els investigadors han estudiat la validesa de les tres formulacions més utilitzades de la llei de Zipf en tots els textos en llengua anglesa (31.075 llibres) de la base de dades del Projecte Gutenberg, i han observat que una d’aquestes formulacions ajusta, amb resultats estadísticament significatius (p>0,05), la freqüència d’aparició de totes les paraules de més del 40% dels llibres de la col·lecció, uns textos que contenen entre 100 i més d’un milió de paraules.
“La llei de Zipf ha generat molt de debat, però sempre bansat-se en la seva validesa en alguns exemples particulars” afirma Álvaro Corral. “Sembla evident que, en l’actual era del Big Data i de les computadores d’altes prestacions, s’haurà d’enfocar els esforços en l’anàlisi de la llei a gran escala, i aquests resultats són un primer pas en aquesta direcció”.
“Encara que la literatura es considera una de les expressions per antonomasia de la llibertat creadora, ni els més grans autors com Shakespeare o Dickens s'escapen a la tirania de la llei de Zipf”, conclou Corral.
En la recerca, publicada recentment a PLOS ONE, ha estat realitzada pels investigadors del CRM Isabel Moreno Sánchez i Francesc Font-Clos sota la direcció d’Álvaro Corral.
El Centre de Recerca Matemàtica (CRM) és un consorci entre la Generalitat de Catalunya, l’Institut d’Estudis Catalans (IEC) i la Universitat Autònoma de Barcelona (UAB).