Most published sensitivity analyses are wrong
Imagine a mathematical model of a process – e.g. the yield of a chemical reaction or the flow through an aquifer, which produces one output, e.g. a yield for a chemical substance, a water flow to stay with the examples, for every combination of input variables. These could be the characteristics of the chemical reagents or the hydrology of the basin. Next imagine that the input variables are uncertain – they can take different values either because they are unknown, e.g. a chemical reaction rate is not known with precision, or because they normally vary in nature, such as e.g. a precipitation intensity. There are thus infinite possible combinations of input variables each giving a different value for the output. By running the model a sufficient high number of times one can have an idea of how the values of the output distribute themselves – what is the mean of the output, its variance and so on. This procedure is customarily called ‘uncertainty analysis’, as it investigates the uncertainty in the output. Next one can ask himself whether all input variables contributes equally to the uncertainty in the output. In fact this is almost never the case, and often many variables can be varied at will with little variation in the output, while a few variables dominate its behaviour. This kind of pursuit is called sensitivity analysis, as it investigates how sensitive the output is to any of its input. Sensitivity analysis may lead to statements like “70% of the variance of the output is driven by factor X4, factor X2 accounts for 25% of the variance, and the remaining 5% is due to the other factors.”
Most of sensitivity analyses (apparently 96 over 100 in 2014) surprisingly suffer from a major shortcoming, up to the point of being useless. They do not combine at all input values, thus leaving unexplored a very large fraction – if not the almost totality – of the possible combinations.
What bizarre procedure may lead to this unhappy outcome? The procedure – only apparently sound - is the following. First, compute the value of the output in correspondence of a central point, where all variables have their ‘best estimate’ or ‘most likely’ value. Then, move each variable in turn away from this central standard, compute the output and use the difference of this to the previous as a measure of sensitivity.
This sounds as rational but its results are only good if the model is linear. When the model is not linear interesting things happen when more than just one variable is moved away from its centre-value. To make an example a chemical reaction may become explosive for particular combination of the inputs, which the procedure above will never ‘see’. Thus a sensitivity analysis done in this way will produce a rather useless ranking of the input factors – e.g. it may miss totally factors which are all important. This is well known, or almost trivial, for statisticians or practitioners of sensitivity analysis, while it remains overlooked by a majority of modellers.
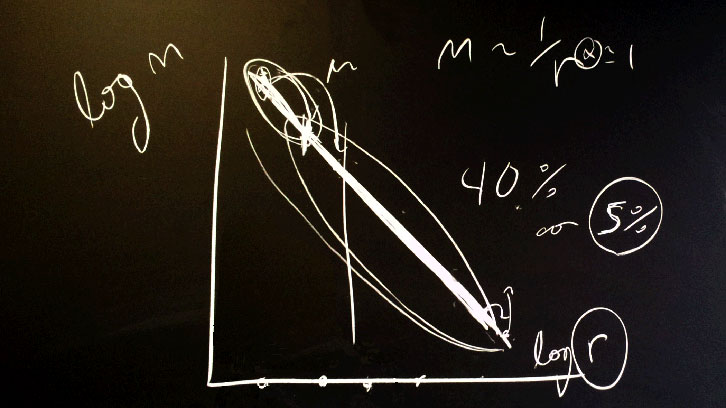
Using a geometric argument our paper shows that for a model with ten factors the typical sensitivity analysis - done by moving one factor at a time, leaves unexplored 99.75% of the possible combination values. This is equivalent to a state of total blindness about what the model really does when allowed to move freely instead of being chained to the centre of its input factors value.
The correct procedure would be to distribute the points as uniformly as possible within the space of all possible combinations of parameters value.
References
Ferretti, F., Saltelli A., Tarantola, S., Trends in Sensitivity Analysis practice in the last decade, Science of the Total Environment. 2016. Special issue on Human and biota exposure. DOI: 10.1016/j.scitotenv.2016.02.133

